Have we been thinking about the pandemic wrong? The effect of population structure on transmission

Summary

• Standard epidemiological models predict that, in the absence of behavioral changes, an epidemic should continue to grow until herd immunity has been reached and the dynamic of the epidemic is determined by people's behavior.

• However, during the COVID-19 pandemic, there have been plenty of cases where the effective reproduction number of the pandemic underwent large fluctuations that, as far as we can tell, can't be explained by behavioral changes.

• While everybody admits that other factors, such as meteorological variables, can also affect transmission, it doesn't look as though they can explain the large fluctuations of the effective reproduction number that often took place in the absence of any behavioral changes.

• I argue that, while standard epidemiological models, which assume a homogeneous or quasi-homogeneous mixing population, can't make sense of those fluctuations, they can be explained by population structure.

• I show with simulations that, if the population can be divided into networks of quasi-homogeneous mixing populations that are internally well-connected but only loosely connected to each other, the effective reproduction number can undergo large fluctuations even in the absence of behavioral changes.

• I argue that, while there is no evidence that can bear directly on this hypothesis, it could explain several phenomena beyond the cyclical nature of the pandemic and the disconnect between transmission and behavior – why the transmission advantage of variants is so variable, why waves are correlated across regions, why even places with a high prevalence of immunity can experience large waves – that are difficult to explain within the traditional modeling framework.

• If the population has that kind of structure, then some of the quantities we have been obsessing over during the pandemic, such as the effective reproduction number and the herd immunity threshold, are essentially meaningless at the aggregate level.

• Moreover, in the presence of complex population structure, the methods that have been used to estimate the impact of non-pharmaceutical interventions are totally unreliable. Thus, even if this hypothesis turned out to be false, we should regard many widespread claims about the pandemic with the utmost suspicion since we have good reasons to think it might be true.

• I conclude that we should try to find data about the characteristics of the networks on which the virus is spreading and make sure that we have such data when the next pandemic hits so that modeling can properly take population structure into account.

The COVID-19 pandemic has been ongoing for more than one year and a half now, but we still don’t understand its dynamic well. What is perhaps more surprising, however, is that the fact that we don’t understand it well is not more widely acknowledged. For the most part, governments continue to rely on projections based on models that have systematically proved to be massively unreliable, while this fact receives almost no attention in the public debate. Occasionally, one can hear people briefly acknowledge that we don’t really understand why waves of infections come and go (typically after the epidemic took a turn that wasn’t predicted by the models used to make projections), but they almost never follow up with a real effort to try and figure out why the pandemic exhibits this cyclical pattern. People often claim that it’s because respiratory infections are “seasonal”, but meteorological variables are not associated with transmission strongly enough to explain this pattern, so in practice this boils down to the claim that infections rates fluctuate over time, which is not a genuine explanation but just a restatement of what is to be explained. In theory, transmission should ultimately be determined by people’s behavior, but the effective reproduction number often fluctuates wildly even when, as far as we can tell with the data we have, there were no behavioral changes.

In this post, I propose that such fluctuations could be the result of population structure, which is mostly ignored in the models used in applied work on the pandemic. Indeed, while standard epidemiological models assume that the virus spreads in a homogeneous or quasi-homogeneous population (i. e. that infectious people have the same probability of infecting anyone else in the population or at least in their age group), this is a very crude idealization. In reality, the virus spreads on a complex network, which depends on people’s patterns of interactions. I show with simulations that, if real populations depart sufficiently from the homogeneous mixing assumption, the effective reproduction number can undergo large fluctuations even in the absence of behavioral changes. I argue that, although we don’t have evidence bearing directly on this hypothesis, in addition to the disconnect between transmission and behavior that has often been observed, it could explain several other puzzling phenomena. Finally, I show that if real populations really have the kind of structure posited by my theory, then the methods used in the literature to estimate the effects of non-pharmaceutical interventions are totally unreliable. Thus, even if that hypothesis turned out to be false, as long as we have good reasons to believe it might be true, we should take the conclusions of studies on the impact of non-pharmaceutical interventions, many of which are of dubious quality even if we ignore the issue of population structure, with a large grain of salt.

What epidemics are supposed to be like according to standard epidemiological models

There are many different approaches to model the spread of infectious diseases, but the most commonly used models are compartment models, which are called that because they divide the population into several compartments and model the way in which individuals move from one compartment into another in the course of the epidemic. For instance, the Susceptible-Infectious-Recovered (SIR) model, which is arguably the most famous epidemiological model, divides the population into 3 compartments. At the beginning of the epidemic, everyone is susceptible, but after the virus is introduced in the population people start infecting each other and move into the infectious compartment, then finally into the recovered compartment when they are no longer infectious and can no longer be infected because they have become immune. Variants of this model can be obtained by adding or removing compartments and transitions between them, which makes this approach very flexible. For instance, the Susceptible-Exposed-Infectious-Recovered (SEIR) model adds a compartment for people who have been exposed but are not yet infectious because they are still in the incubation period, as well as a transition between the exposed and infectious compartments. Of course, the SIR model can also be adapted to take vaccination into account, which reduces the share of the population susceptible to infection.

In this post, I will use a closely related model, which is essentially a stochastic, discrete-time version of the SIR model with overdispersion. Don’t worry if this sounds like gibberish to you, the model is actually very simple and the way in which it works can be explained without complicated jargon. The key quantity governing the dynamic of the epidemic in the model is the basic reproduction number. It’s the average number of people that someone who is infected would infect during their infectious period if everyone in the population were susceptible. It must be distinguished from the effective reproduction number, which is the actual number of people that people who are infected will infect on average. The effective reproduction number is always lower than the basic reproduction number, because not everyone is susceptible in the population, so some people that would have been infected after interacting with someone infectious will not actually be infected because they are no longer susceptible. The model assumes that everyone has immunity after they have been infected and that everyone in the population interacts with everyone else randomly. Thus, if the basic reproduction number is 3 and at one point during the simulation 50% of the population has already been infected, the effective reproduction number at that point is only 1.5, because on average 50% of the people that infectious people interact with can no longer be infected. At the beginning of the simulation, the population is seeded with a few infected people to get the epidemic started. On each day, the model randomly draws the number of people that each person infected on that day will eventually infect from a negative binomial distribution with a mean equal to the effective reproduction number on that day and a dispersion parameter of 0.1, so as to model superspreading.¹ Then, for each secondary infection caused by a person infected on that day, it randomly draws how much time later this secondary infection takes place from a gamma distribution with a mean of 4.8 days and a standard deviation of 1.7 days.² This process is repeated until the end of the simulation.

This graph shows how a typical epidemic unfolds in that model with a basic reproduction number of 3 in a population of 10 million:

As we shall see, a crucial assumption of this kind of model, which is called the homogeneous mixing assumption, is that people interact and infect each other randomly. However, as long as that assumption holds and even when it’s somewhat relaxed, a compartment model will always generate a qualitatively similar epidemic if the basic reproduction number remains constant and the immunity acquired by people who have recovered doesn’t wane. In other words, while the height of the curve at the peak and the area under it may vary depending on what assumptions were made, it will always have this kind of shape as long as the basic reproduction number remains constant, immunity doesn’t wane and the homogeneous mixing assumption or something close enough to it holds.

As we have seen, the basic reproduction number is the number of people that each infected individual will infect on average when everyone in the population is susceptible. It depends on how many contacts infectious people have and how often those contacts result in transmission of the virus. Thus, in a framework where immunity is assumed to be permanent and the homogeneous mixing assumption is made, the basic reproduction number only depends on people’s behavior. It goes up when people have more contacts with each other or have contacts that are more likely to result in transmission of the virus and goes down if they have fewer contacts or have contacts that are less likely to result in the transmission of the virus. This is a key assumption of the standard modeling framework, so it’s important to understand this point, because as we shall see shortly there are good reasons to doubt that it’s true. As I already noted, in the simulation that was used to generate the epidemic depicted on the graph shown above, the basic reproduction number was assumed to be equal to 3. A population of 10 million was seeded randomly with a few infections during the first 30 days of the simulation and some of them started chains of infections that eventually resulted in the large epidemic shown in the graph. The basic reproduction number was assumed to remain constant over time, which is equivalent to assuming that people didn’t change their behavior during the course of the epidemic or at least not in a way that affected the basic reproduction number.

As you can see on the graph, during the initial phase of the epidemic, the daily number of infections — which is called “incidence” — is growing exponentially. This makes sense because, while everyone or almost everyone is still susceptible, each person infects 3 people on average after being infected, each of whom then go on to infect 3 people on average, etc. However, as the epidemic grows, the average number of people infected by infectious individuals, which as we have seen is called the effective reproduction number (as opposed to the basic reproduction number that would obtain if everyone were susceptible), goes down since more and more of the people they interact with and would have infected when everyone was susceptible have immunity because they have already been infected previously. Eventually, the epidemic reaches a point where each person only infects 1 other person after they have been infected, which is called the herd immunity threshold. If the basic reproduction number is 3 as I have assumed in the simulation, the herd immunity threshold is reached when 2/3 of the population has already been infected and is no longer susceptible, because at this point 2 out of 3 people that would have been infected by each infectious person have immunity and can’t be infected anymore. Once the herd immunity threshold has been crossed, incidence starts to go down, until eventually it reaches zero and the epidemic is extinguished.

This is what happens when the basic reproduction number stays constant, but things are different if people voluntarily change their behavior or are forced to do so by the government.³ For instance, suppose that initially the basic reproduction number is 3, but that on the 50th day of the simulation the government declares a lockdown for 60 days, which temporarily brings down the basic reproduction number to 0.75 before it goes back to 3 after the lockdown is lifted.⁴ This graph shows the result of a simulation under this scenario with the same model as before:

As you can see, after the lockdown comes into effect, incidence starts to go down.⁵ However, exponential growth resumes as soon as the lockdown is lifted, which results in a very large second wave. This wave only starts receding when the herd immunity is reached, which as before happens when 2/3 of the population has been infected, since after the lockdown is lifted the basic reproduction number goes back to 3 because we’re assuming that people only changed their behavior in response to restrictions.

As I already noted, there are many variants of the SIR model, but they exhibit the same qualitative behavior in almost every case. This is true even when the homogeneous mixing assumption is somewhat relaxed. For instance, the herd immunity threshold in the SIR model is (where is the basic reproduction number), but it’s lower in a model that divides the population into groups of people who differ in how much social activity they have. However, even in such a model, incidence keeps growing until the herd immunity threshold is reached and can no longer grow after that threshold has been reached. Thus, while the height of the epidemic curve and the area under it may be different in different models, as long as they assume that immunity doesn’t wane and do not depart too much from the homogeneous mixing assumption, the epidemic curve always has the same basic shape, with a phase of exponential growth that gradually slows until the peak corresponding to the herd immunity threshold is reached, after which incidence starts decreasing until it reaches zero and the epidemic is extinguished. Moreover, even if the basic reproduction number is temporarily reduced by non-pharmaceutical interventions or voluntary behavior change and the effective reproduction number drops below 1 in such a model, incidence starts growing again as soon as the basic reproduction number goes back to its previous level unless the herd immunity threshold has been reached or the number of infected people has dropped to zero before that.⁶

Standard epidemiological models fail to explain the dynamic of the COVID-19 pandemic

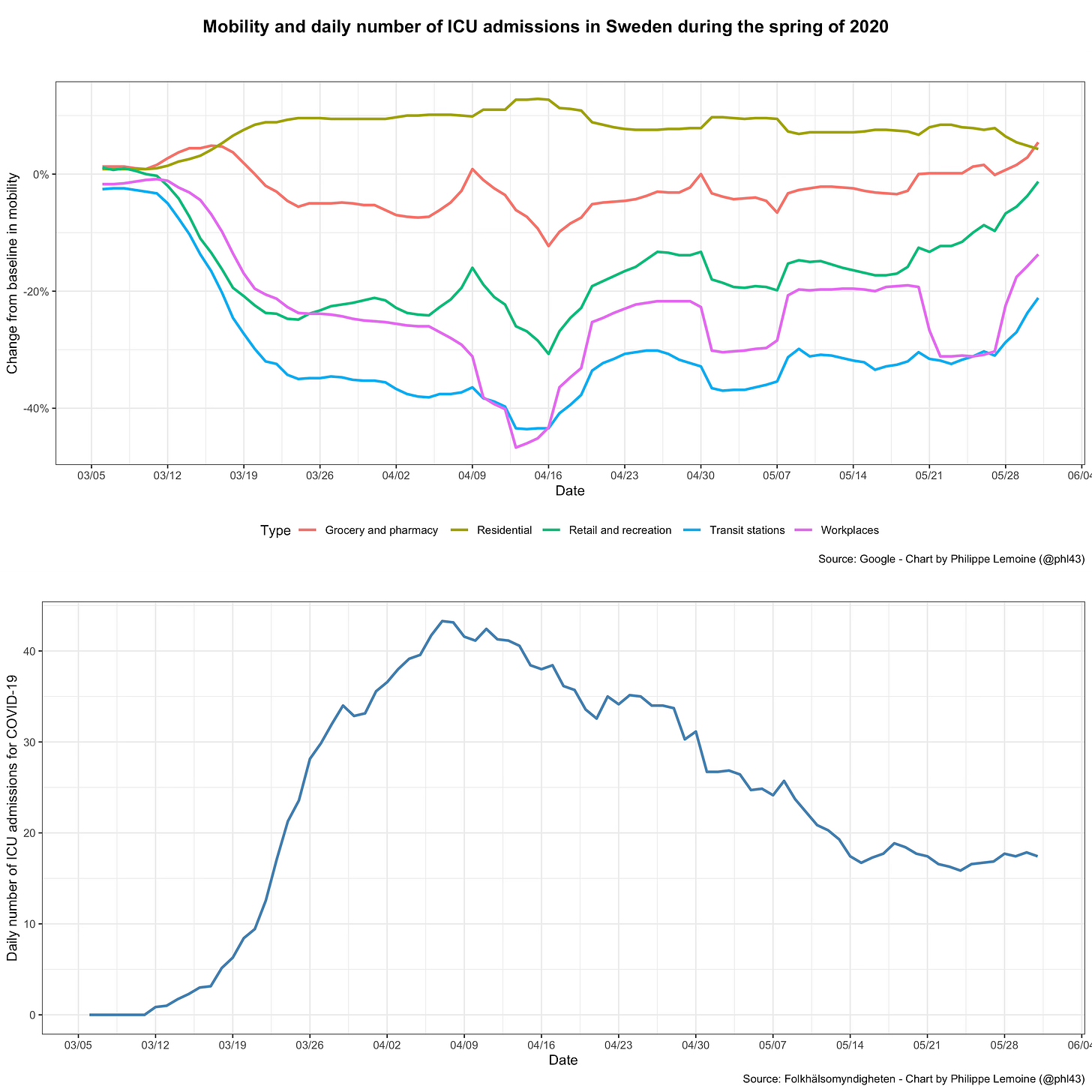
As we have just seen, based on the SIR model and most of its variants, we would expect the COVID-19 pandemic to exhibit a specific type of dynamic. In particular, as long as the population is still far from the herd immunity threshold, the epidemic should grow quasi-exponentially unless people change their behavior in a way that affects the basic reproduction number. However, if we look at real data during the COVID-19 pandemic, we see that actual epidemic behavior radically departs from this prediction. First, as I noted previously, there are many cases in which incidence started to fall long before the herd immunity threshold could plausibly be assumed to have been reached and despite the absence of a lockdown or other stringent legal restrictions. The most famous example is what happened in Sweden during the first wave, but it’s not a very good example if we’re trying to show that standard epidemiological models can’t explain the data because there is very good evidence that people in Sweden engaged in massive voluntary behavioral changes despite the absence of stringent restrictions:

As you can see, the daily number of ICU admissions for COVID-19 started to fall in early April, which suggests that incidence started to fall about 2 weeks before that.⁷ But as I noted above, this graph also shows a large reduction of mobility around the same time. Thus, if this reduction of mobility was associated with behavioral changes that resulted in a reduction of the reproduction number (which is likely because it’s hard to imagine that such a large reduction in mobility was not accompanied by a reduction in the number of contacts people had with each other), it’s not surprising that incidence fell despite the lack of stringent restrictions, since that’s exactly what standard epidemiological models in which the basic reproduction number is allowed to vary predict.⁸

However, there are many examples where the same thing happened, but without any evidence that voluntary behavioral changes could explain why incidence started to fall even though herd immunity was still a long way. For instance, it happened in Florida during the summer of 2020, where there was a large wave of infections that peaked in the middle of July:

A variety of restrictions were in place during this period in Florida, which varied on a county-by-county basis, but in most places they were implemented in June or at the beginning of July and remained in place until after the wave had peaked, so non-pharmaceutical interventions can’t explain why incidence started falling in mid-July.⁹ Moreover, as you can see on the chart, while mobility was significantly reduced compared to the pre-pandemic period, there was virtually no change in mobility except for a temporary drop around the Fourth of July. I could make the same point about the wave of infections that Florida experienced last winter, which receded in January before vaccination could possibly have made any difference, while there were virtually no restrictions and despite the fact that mobility didn’t change during that period except for Christmas and New Year’s Day.

Another example is what happened in Spain last winter when the country experienced a very large wave, yet the government refused to order another lockdown, as it had during the first wave. Local governments did put in place a variety of restrictions, but the national government prevented them from ordering a regional lockdown and, in some regions, restrictions remained minimal during most of the period. In particular, this was the case in Madrid, but it didn’t prevent incidence from peaking around the same time as in the rest of Spain:

The only significant change in the legal restrictions that applied in Madrid during this period was a set of new rules, including a curfew between 11 pm and 6 am, that came into effect on January 18, but taking into account the incubation period the peak of infections almost certainly happened before that. Moreover, as you can see in the upper panel of the chart, this didn’t have any detectable effect on mobility. The fact that incidence started to fall around the same time in Spain, despite the wide variety of restrictions that local governments imposed in different regions, also suggests that government intervention wasn’t a key factor. If we look at mobility, which captures behavioral changes regardless of whether they were voluntary or induced by restrictions, there was a drop associated with Christmas, New Year’s Day and the Epiphany, as well as a significant fall that lasted for about a week after the Epiphany and was presumably caused by the snowstorm that paralyzed Madrid for several days at the time. In theory, this could have temporarily reduced transmission, but since mobility started to reverse to previous levels as soon as the snow was cleared from the streets this reduction should have been temporary and standard epidemiological models predict that epidemic growth should have quickly resumed. However, that is not what happened, since incidence continued to fall after that and didn’t rise again until the end of March. Vaccination also couldn’t possibly explain why the epidemic receded since it was still progressing at a very slow pace in Spain at the time and, even by the end of January, only 0.8% of the population was fully vaccinated.

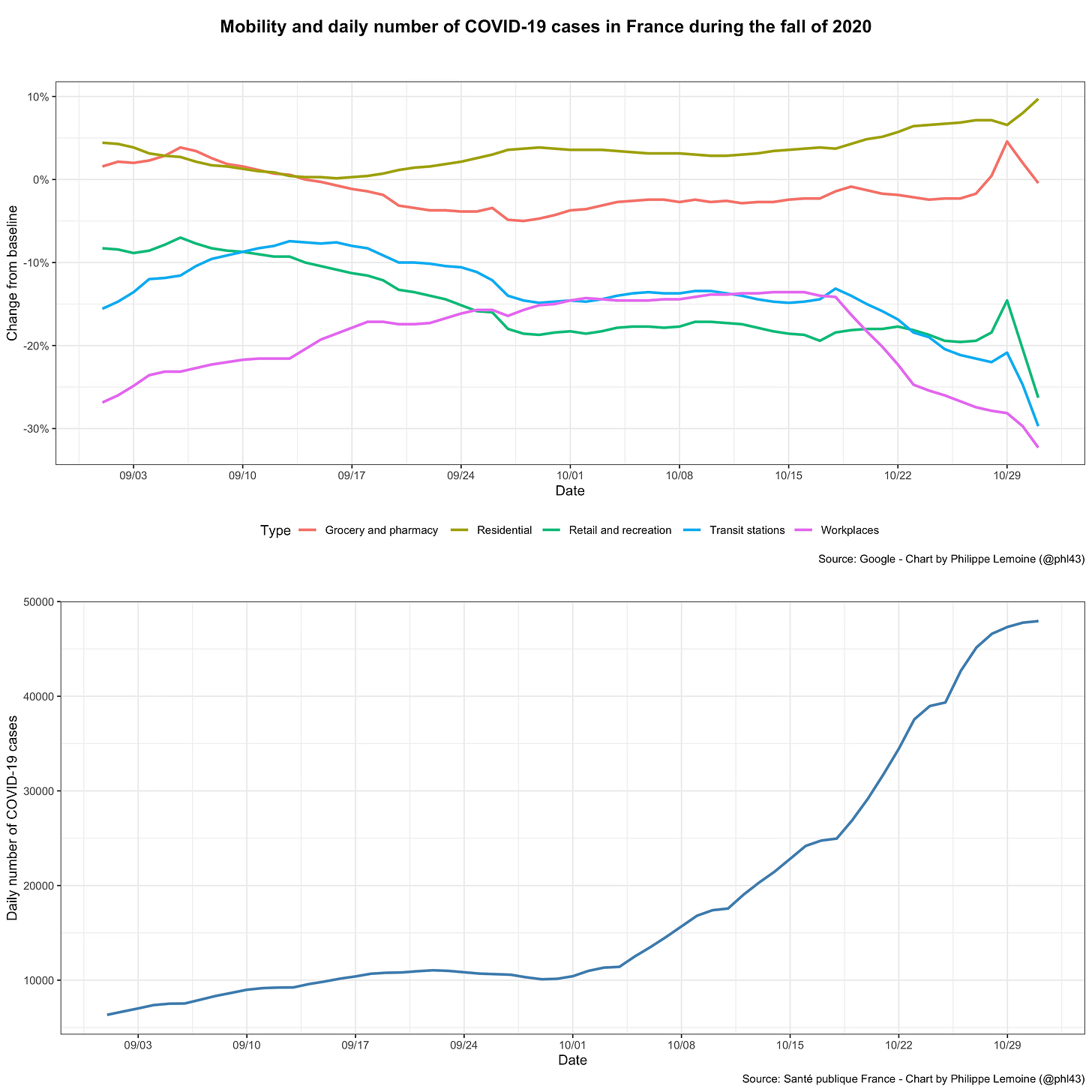
Thus, incidence often starts falling long before it should according to standard epidemiological models, but it also starts to rise when, according to the same models, it should not. The debate has focused on what makes waves of infections recede, but if we’re trying to understand the dynamic of the epidemic, the question of why incidence rises when it does is just as important. Sometimes, it seems that incidence starts blowing up for no particular reason, since none of the factors that are assumed to govern the dynamic of the epidemic by standard epidemiological models have changed. For instance, France experienced a large wave of infections last fall, yet neither changes in restrictions nor changes in mobility can explain why the epidemic growth exploded when it did:

As you can see, incidence plateaued in September before suddenly exploding in October, but there were no non-pharmaceutical interventions until mid-October and mobility doesn’t seem to have changed before that.

In this case, I think it’s illuminating to also compare mobility to the effective reproduction number and not just the daily number of cases, because it illustrates the fact that restrictions and voluntary behavior changes can’t explain the way in which transmission changes over time:

As you can see, the effective reproduction number fell sharply in September before increasing rapidly at the beginning of October (which led to a large wave of infections and ultimately the second lockdown), but again there were virtually no restrictions until mid-October in France and it doesn’t seem that changes in mobility can explain those fluctuations either.¹⁰

I could literally go on for hours about other similar examples, which are difficult to reconcile with the way epidemics are supposed to behave according to standard epidemiological models, but you get the idea. In general, when looking at data on the COVID-19 pandemic, it’s striking how volatile the effective reproduction number is and how little of those fluctuations make sense within a framework that assumes that, as long as the population isn’t close to herd immunity, the dynamic of the epidemic is driven by changes in behavior, whether voluntary or induced by non-pharmaceutical interventions. This conclusion is not the result of cherry-picking, since it’s also clear when you perform more systematic analyses. Indeed, while many studies reported a strong correlation between mobility and epidemic growth early in the pandemic, this association became very weak almost everywhere after the first wave.¹¹ There seem to be other factors besides changes in behavior that have a large effect on the dynamic of the epidemic. However, the overwhelming majority of epidemiological models used to study the pandemic don’t take into account any other factors, so it’s unsurprising that they have performed so abysmally. It’s well-known that, when incidence is low, stochastic factors can play a large role, but this can’t be the explanation for the large fluctuations of the reproduction number we observe in the data that are not accounted for by changes in behavior since, as we have just seen, such fluctuations were often observed during periods when incidence was high.

Among the factors that have been put forward to explain the fluctuations of the effective reproduction number, this only leaves meteorological variables. However, while I do not doubt that meteorological variables affect transmission, I don’t think they can explain the large fluctuations that the effective reproduction number often undergoes even in the absence of behavioral changes. First, while several studies have found a relationship between meteorological variables and the effective reproduction number, the association seems relatively weak.¹² Indeed, places with very similar climates have experienced waves of infections at very different times of the year, while places with completely different climates have experienced waves at the same time, which should already make clear that meteorological variables only have a limited impact even without looking at the data in a more systematic way. Moreover, to the extent that meteorological variables affect transmission, we expect their effect to be at least partly mediated by people’s behavior. Indeed, meteorological variables can in theory have both a direct and indirect effect, but only the former is independent from behavior. The direct effect is the effect that meteorological variables have on the mechanism of transmission at the biochemical level, while the indirect effect is the effect they induce by causing behavioral changes. Indeed, as we have seen above in the case of the snowstorm that paralyzed Madrid for several days last January, weather affects people’s behavior, which in turn can affect transmission. Since part of the effect of meteorological variables on transmission is mediated by people’s behavior, it’s even more unlikely that meteorological variables could explain why the effective reproduction number often undergoes large fluctuations even in the absence of meaningful behavioral changes. This suggests that standard epidemiological models can’t be fixed by taking into account more variables, but that a more fundamental change of framework is called for.

Of course, if you are really committed to standard epidemiological models, you can always come up with a story to reconcile the data with those models. For instance, in my discussion so far, I have used mobility as a proxy for the behavioral variables that affect transmission, but one could object that data on mobility don’t reflect the relevant behavioral changes and that it’s therefore wrong to infer from the weak association between mobility and epidemic growth that behavior can’t explain the dynamic of the epidemic. It could be that, with better data on people’s behavior, we’d find a stronger association between behavioral changes and the effective reproduction number. A recent study based on GPS tracking data from over 1 million cellphones in Germany suggests that, with more fine-grained data, we may indeed be able to do that. The authors used the data to determine when people were physically close to each other, considered it a contact when they remained close for long enough and used that to construct a graph of people’s contacts. Based on that graph, they were able to compute not only the average number of contacts over time, but also what they call a “contact index” that takes into account both the average number of contacts and its variance. They also computed this index because theoretical results suggest that heterogeneity of contacts and not just the mean number of contacts people have affect the epidemic’s reproduction number. They show that, while the average number of contacts is poorly correlated to the effective reproduction number after the first wave, the contact index remained predictive of the effective reproduction number after that.¹³ Of course, this study has many limitations (starting with the fact that it’s limited to data about Germany), but I think it’s nevertheless a very important paper that has unfairly been ignored and hopefully this post can help rectify that.

This study provides some evidence for the claim that, while aggregate mobility data is not very predictive of the effective reproduction number, we’d be able to find a stronger association between transmission and behavior if we had more fine-grained data on the latter. However, while I have no doubt that mobility data are a very imperfect proxy for the relevant behavioral changes and that we’d find a stronger association between the effective reproduction number and behavior with better data, the disconnect between mobility and epidemic growth is so extreme in so many cases that I find this response totally unconvincing if it’s meant to imply that, except for a small part of the variability that can be explained by factors such as meteorological variables, behavioral changes are sufficient to explain the fluctuations of the effective reproduction number. In general, it’s always possible to protect any theory against falsification if you’re willing to add enough epicycles to it, but it doesn’t mean that it’s reasonable to do so. If there were just a few anomalies in the data, it would make sense to explain them away by assuming that a few unknown factors that generally play a small role sometimes conspire to falsify standard epidemiological models that don’t take them into account, but anomalies are ubiquitous so I think it’s clear that something else is going on here.¹⁴ Everywhere waves come and go in a way that is impossible to reconcile with the predictions of standard epidemiological models without tying yourself into knots and the effective reproduction number frequently undergoes large fluctuations that can’t be explained by changes in behavior. While epidemiologists have mostly ignored this fact and continue to use models that have systematically and massively failed, I think it’s time to accept it and try to understand what, in the absence of meaningful behavioral changes, could explain the large fluctuations of the effective reproduction number that we have observed.¹⁵

Population structure as the missing piece of the puzzle

At this stage, we seem to be faced with a dilemma. On the one hand, as we have seen, the effective reproduction number of the epidemic frequently undergoes large fluctuations even in the absence of behavioral changes. On the other hand, we have strong theoretical reasons to expect that ultimately transmission depends on people’s behavior, since we know that SARS-CoV-2 transmits by contact. Thus, it seems that any theory that can explain why the effective reproduction number can undergo large fluctuations even in the absence of meaningful behavioral change must deny this basic fact about the mechanism of transmission, making it a non-starter. In this section, I will try to square this circle by presenting a theory that, while consistent with the fact that SARS-CoV-2 is transmitted by contact and therefore that ultimately transmission depends on people’s behavior, explains why large fluctuations of the effective reproduction number can nevertheless occur even in the absence of meaningful behavioral changes. The first thing to consider is that, from the fact that SARS-CoV-2 is transmitted by contact, it doesn’t follow that large fluctuations of the effective reproduction number can only result from large behavioral change. In fact, I have already implicitly acknowledged that fact above when I said that meteorological variables probably affect transmission, even if their effect doesn’t seem large enough to explain the large fluctuations of the effective reproduction number that we frequently observe even in the absence of behavioral changes.¹⁶ Another example of a factor that could affect transmission even if people don’t change their behavior is the emergence of more transmissible variants. As I argued previously, I think that Alpha’s and Delta’s transmissibility advantages over the previously established strains have been vastly overestimated, but you don’t have to agree with me on that to agree that it can’t be the whole story behind the disconnect between transmission and behavior. Indeed, as the examples I used above show, the effective reproduction number has often undergone large fluctuations in the absence of meaningful behavioral changes even when the distribution of variants remained stable. So there must be another factor that explains this phenomenon and, in this section, I will propose that it’s population structure.

As we have seen, in order to study the spread of infectious diseases, epidemiologists use models that make various simplifying assumptions. In particular, they typically assume a homogeneous mixing population, which means that contacts between people are totally random, so everyone is equally likely to infect everyone else if they are infected.¹⁷ However, this assumption is totally unrealistic, because in the real world transmission occurs in a highly structured population and contacts are not random. If you are infected, the probability that you are going to infect most people in the population is effectively zero, because you’ll never have any contact with them. Of course, there are many people you will never have any contact with, but whom you could nevertheless indirectly infect by starting a chain of infections that goes through them, but for most people the probability that this will happen is infinitesimal, whereas it’s much higher for people you interact with often because they are your colleagues, friends, members of your family, etc. and people who frequently interact with them. In reality, the virus doesn’t spread in a homogeneous mixing population, but in a highly structured one where each individual has different patterns of interactions with different people. How the virus spreads depends on who interacts with whom, how often they interact and what type of interaction they have, since those facts determine what chains of infections can exist and how likely each of them is depending on where the virus starts from in the population.

Thus, while standard epidemiological models represent the population as a collection of particles that interact randomly with each other, it’s better seen as a complex network where nodes are individuals and edges represent potential interactions between them that could result in transmission. Each edge in the network has a weight that indicates how easily transmission can occur along that edge if one of the individuals it connects happens to be infectious, which is determined by the frequency and nature of the contacts between them. Epidemiologists of infectious diseases have produced a voluminous literature on models that assume a virus spreads on these kinds of networks, so it’s not as if they didn’t know that real epidemics don’t spread in a homogeneous mixing population and hadn’t studied how population structure can affect transmission, but this literature had essentially no effect on applied work during the pandemic, perhaps because the kind of data that would be necessary to model real epidemics in that way is almost never available.¹⁸ Yet I think that population structure could hold the key to the mystery I have identified above, namely that the effective reproduction number often undergoes large fluctuations that, as far as we can tell, can’t be explained by changes in people’s behavior. Indeed, what I’m proposing is that we can solve this mystery by postulating that the network on which the epidemic spreads has what in network science is called “community structure”, which means that it can be divided into subnetworks whose nodes are internally densely connected while the subnetworks are only loosely connected to each other.

To illustrate this concept, here is a graph I found in this paper that shows the friendship network of a few thousand people on Facebook, where community structure is clearly visible:

Of course, the networks on which the COVID-19 epidemic spreads are far more complicated, since they can involve millions of people. Moreover, the edges between nodes don’t have the same meaning, since you can be friends with someone on Facebook but never have any interaction with them that could result in transmission of the virus and you can have that kind of interaction with someone you aren’t friends on Facebook with. But fundamentally what I’m proposing is that, when the epidemic spreads in a country, it does so in a network that has this kind of structure.

But how would that explain why the effective reproduction number of the epidemic can undergo large fluctuations even when people’s behavior doesn’t change? Well, if the virus is introduced in a network of this type, it will spread easily within the subnetwork where it has been introduced, but it will have a harder time leaving that subnetwork to spread into others, because subnetworks are loosely connected to each other. As it spreads through a subnetwork, the prevalence of immunity will increase in that subnetwork and, unless it manages to reach another subnetwork from there, the effective reproduction number of the epidemic will go down. When the virus is introduced in another subnetwork where the prevalence of immunity is low, either because that subnetwork has been seeded from the outside or because the virus managed to reach it from another subnetwork through one of the edges connecting them, the effective reproduction number will go up again and so will incidence, until that subnetwork is also saturated. Thus, if the population has that kind of structure, waves of infections will tend to be restricted to one or a few subnetworks, which in turn would explain why they come and go even when people don’t change their behavior. On this hypothesis, the virus is still transmitted by contact and therefore transmission still depends on people’s behavior, so it’s consistent with what we know about the basic mechanics of transmission, but how behavior at the individual level translates into the effective reproduction number at the aggregate level depends on population structure. This theory can therefore solve the dilemma I identified at the beginning of this section of the apparent impossibility of reconciling our knowledge of the mechanics of transmission at the individual level with the data at the aggregate level. In short, according to it, population structure was the missing piece of the puzzle.

Simulating the effect of population structure on transmission

The claims I just made about how population structure affects transmission seem intuitively plausible, but intuition can be misleading, so in this section I’m going to present the result of simulations that confirm that, when the network that encodes the information about people’s interactions can be divided into subnetworks that are internally densely connected but only loosely connected to each other, the effective reproduction number of the epidemic can undergo large fluctuations even if we assume that people’s behavior doesn’t change.¹⁹ Instead of simulating the spread of the virus on a network of individuals, which is very computationally intensive if the network is large, I assumed that parts of that network could be considered homogeneous mixing populations and modeled the spread on a network of subpopulations. I construct the network in such a way that it can be divided into subnetworks containing subpopulations that are well-connected to each other, but only loosely connected to subpopulations in other subnetworks. Since I assume that each subpopulation in the network is approximately homogeneous mixing, the spread of the virus within each subpopulation is modeled with the stochastic, discrete-time SIR-type model I described in the first section. However, people who have been infected in one subpopulation can spend their infectious period in another, as long as the subpopulation to which they belong is connected to it. I came up with this approach on my own when I started thinking about this, but it turns out that it’s similar to what epidemiologists call metapopulation modeling, which is not surprising since it’s a very natural way of modeling population structure. However, in the literature on that kind of models, subpopulations are often interpreted as spatially separated from each other, whereas for reasons I will explain later I make no such assumption.

I assume the population is divided into 100 subnetworks and randomly draw the number of subpopulations each of them contains from a Poisson distribution with a mean of 100. This resulted in a network of 10,105 subpopulations distributed across 100 subnetworks. The size of each subpopulation is randomly drawn from a discrete power law with a minimum size of 250 and a scaling parameter of 2.9. The result is that subpopulations have a size of about 520 on average, for a total population of approximately 5.2 million, but the vast majority of subpopulations are smaller than that while a few are much larger because power laws are fat-tailed. Each subnetwork is generated randomly using a method called the configuration model.²⁰ Roughly, the number of edges connected to each node — which is called the degree of that node — is randomly drawn from a Poisson distribution with a mean of 5, then nodes are connected to each other randomly so as to respect this pre-defined degree distribution.²¹ Once the subnetworks have been generated, it remains to connect them to each other. In order to do so, for each subnetwork, I first randomly draw the number of edges connecting a node in that subnetwork to a node in another subnetwork, which can be seen as the analogue of the degree of a node for subnetworks, from a Poisson distribution with a mean of 5. Then, I randomly pick a node in one subnetwork and connect it to a randomly chosen node in another subnetwork, so as to respect this pre-defined degree distribution.²² The result is a network that can be divided into subnetworks that are internally densely connected, but only loosely connected to each other.²³

Here is a visualization of the network that was generated by this procedure and used for the simulation whose results I’m going to present shortly:

In order to make the community structure easier to visualize, I assigned a different color to each subnetwork and used a graph drawing algorithm to cluster the nodes by subnetwork.²⁴

Connectivity in the relevant sense doesn’t only depend on the number of edges connecting different subpopulations, but also on the probability that someone who belongs to one subpopulation will travel along one of those edges to another subpopulation and spend their infectious period over there.²⁵ Thus, in order to model that, each edge is assigned a weight that corresponds to the probability that someone who has been infected in one subpopulation will travel along that edge and spend their infectious period in another subpopulation. I used a weight of 0.05 for within-subnetwork edges and a weight of 0.0001 for between-subnetwork edges. In other words, infectious people in one subpopulation have a 5% chance of spending their infectious period in each of the subpopulations in the same subnetwork to which it’s connected, while they have a probability of 1 in 10,000 of spending their infectious period in each of the subpopulations in a different subnetwork to which it’s connected. Thus, the virus can travel much more easily within subnetworks than between them, since nodes within the same subnetworks are both more densely connected and the edges connecting them have a greater weight than nodes belonging to different subnetworks. Nevertheless, by the time a subnetwork has been completely saturated by the virus, the probability that it has traveled to another subnetwork from there — where it may or may not start a large outbreak — is about 25%, so it’s hardly impossible and will often happen.²⁶

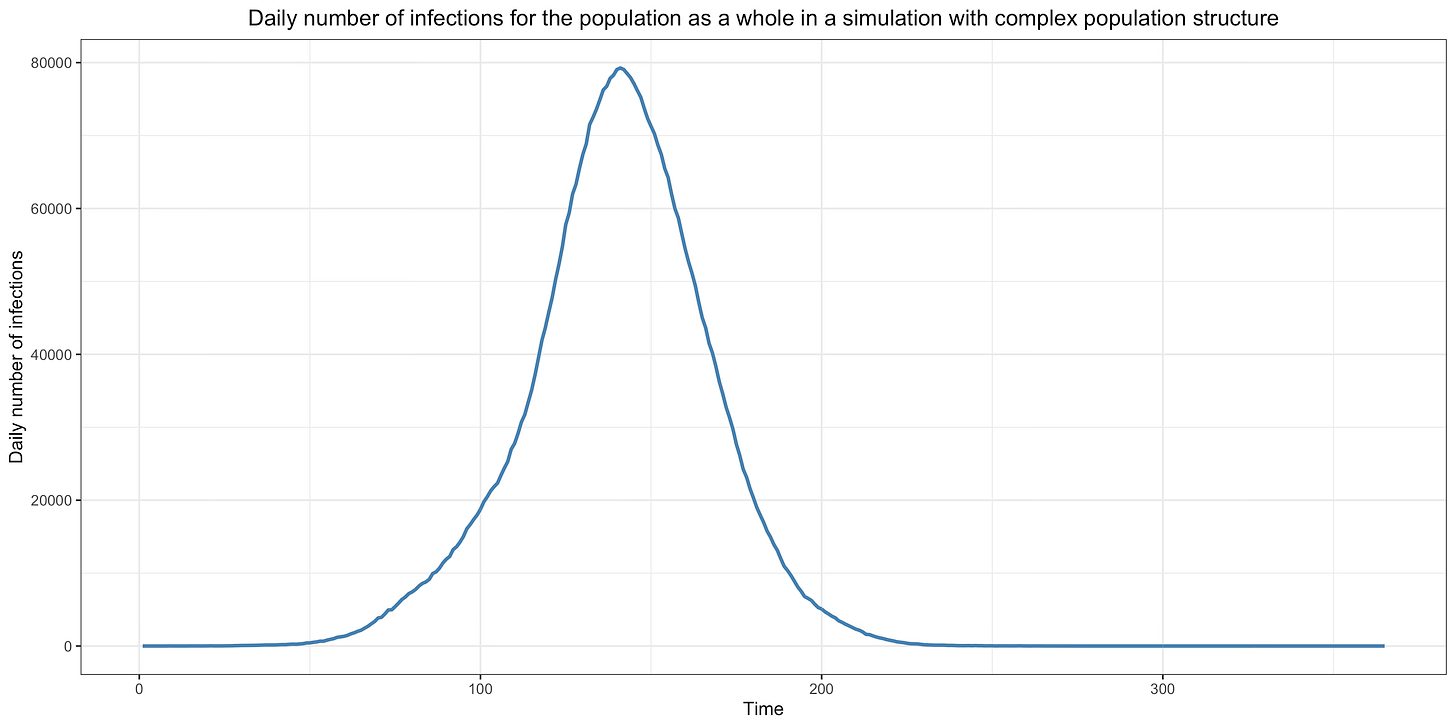
I seed the population randomly at a constant rate for the whole duration of the simulation and, on each day, infected people from the outside are randomly distributed across subpopulations.²⁷ You can think of the population I’m modeling as a country that is being continuously and randomly seeded from abroad at a constant rate. This isn’t very realistic, because in reality the rate at which a country is seeded depends on the state of the epidemic in other countries to which it’s connected and which subpopulation is seeded is not random but depends on what connections they have to foreign countries, but it’s good enough for my purposes in this post.²⁸ The basic reproduction number in each subpopulation was randomly drawn from a normal distribution with a mean of 2.5 and a standard deviation of 0.1 and was assumed to stay constant for the duration of the simulation. Here is a graph that shows the results of the simulation at the level of the population as a whole:

As you can see, at the aggregate level, the effective reproduction number undergoes large fluctuations and several waves of infections come and go, yet behavior didn’t change since we assumed a constant basic reproduction number in each subpopulation and the fluctuations of the effective reproduction number at the aggregate level are purely the result of population structure.

In order to help you get a more intuitive grasp of what is happening, I made this animation that shows how the virus spreads across subpopulations, which are represented by rectangles whose area is proportional to their size inside larger rectangles that represent the subnetworks to which they belong:

As you can see in this animation, once a subpopulation is invaded, the virus quickly spreads to the other subpopulations in the subnetwork to which it belongs. Different subnetworks are invaded at different times, either because the virus managed to spread to them from another subnetwork or because they were seeded from abroad, so what we are seeing at the level of the population as a whole is really the result of aggregating several distinct though linked epidemics. By the end of the simulation, only 27.6% of the population has been infected. Yet, as you can see in that animation, many subnetworks are still untouched by the time it’s over. Thus, if any of them were seeded with the virus, it would likely result in another wave.

Within each subpopulation, the epidemic is progressing as standard epidemiological models predict and if we plotted the epidemic curve it would look like the curve I showed in the first section, but once aggregated they produce something completely different. When the virus is spreading in subpopulations where most people are susceptible, the effective reproduction number for the population as a whole goes up, but it goes down if most of the infections are taking place in subpopulations where a lot of immunity has accumulated. Of course, the accumulation of immunity in some subpopulations can also be more or less balanced out by the fact that the virus started to spread in subpopulations where almost everyone is susceptible because they had so far been spared, in which case the effective reproduction number for the population as a whole remains pretty stable. Depending on the topology of the network and stochastic factors, the model can produce all sorts of epidemic curves at the aggregate level, not just waves that come and go in relatively quick succession but also long periods during which incidence remains high, as we have also seen in some countries. But this variety of epidemic behavior at the aggregate level has nothing to do with behavioral changes, since at the level of subpopulations behavior and therefore the basic reproduction number is assumed to be constant. Thus, simulations confirm that, if the population is divided into networks of subpopulations that are internally densely connected but only loosely connected with each other, the effective reproduction number can undergo large fluctuations even if people’s behavior doesn’t change, as seems to happen in the real world.

Unsurprisingly, if we increase the connectivity between subnetworks enough, the model behaves more like a model with homogeneous mixing. For instance, if I use the same method to generate a network but multiply the average number of edges between subnetworks by 10 and the weight of those edges by 100, I obtain this epidemic:

However, unless we increase connectivity between subnetworks a lot, the model’s behavior remains very different from that of a model with homogeneous population mixing and, as we shall see, this has radical implications.

The relationship between the model and the real world

Of course, the fact that simulations based on this model generate epidemics that are similar to real data doesn’t mean that the model accurately describes reality and, to be clear, I have no doubt that it leaves out a lot of factors that matter. First, even if I’m right that populations have the sort of structure posited by the model, it’s certainly not the case that, as the model assumes, people’s behavior doesn’t change in a way that affects transmission. Indeed, as I already noted, the fact that the effective reproduction number sometimes undergoes large fluctuations even in the absence of behavioral changes doesn’t mean that behavioral changes doesn’t affect transmission. Not only can it do so by changing the basic reproduction number at the level of subpopulations, but it can also do so by modifying the network. Indeed, while I have assumed for the simulation that the network was constant, a more realistic model would use a time-varying network where, as people change their behavior, some edges can appear or disappear and the weight associated to them can change. I have only assumed that the basic reproduction number at the level of subpopulations was constant and that the network didn’t change over time because I wanted to show that, even in the absence of behavioral changes, population structure alone could result in large fluctuations of the effective reproduction number, but I obviously don’t believe that population is the only factor and that people’s behavior doesn’t matter. In fact, not only is the hypothesis that population structure explains some of the fluctuations of the effective reproduction number not inconsistent with the hypothesis that behavioral changes does, but they are complementary because, as I just noted, taking into account population structure allows one to see that behavior can affect transmission not just by modifying the rate at which transmission occurs along the edges of the network but also by modifying the network itself.

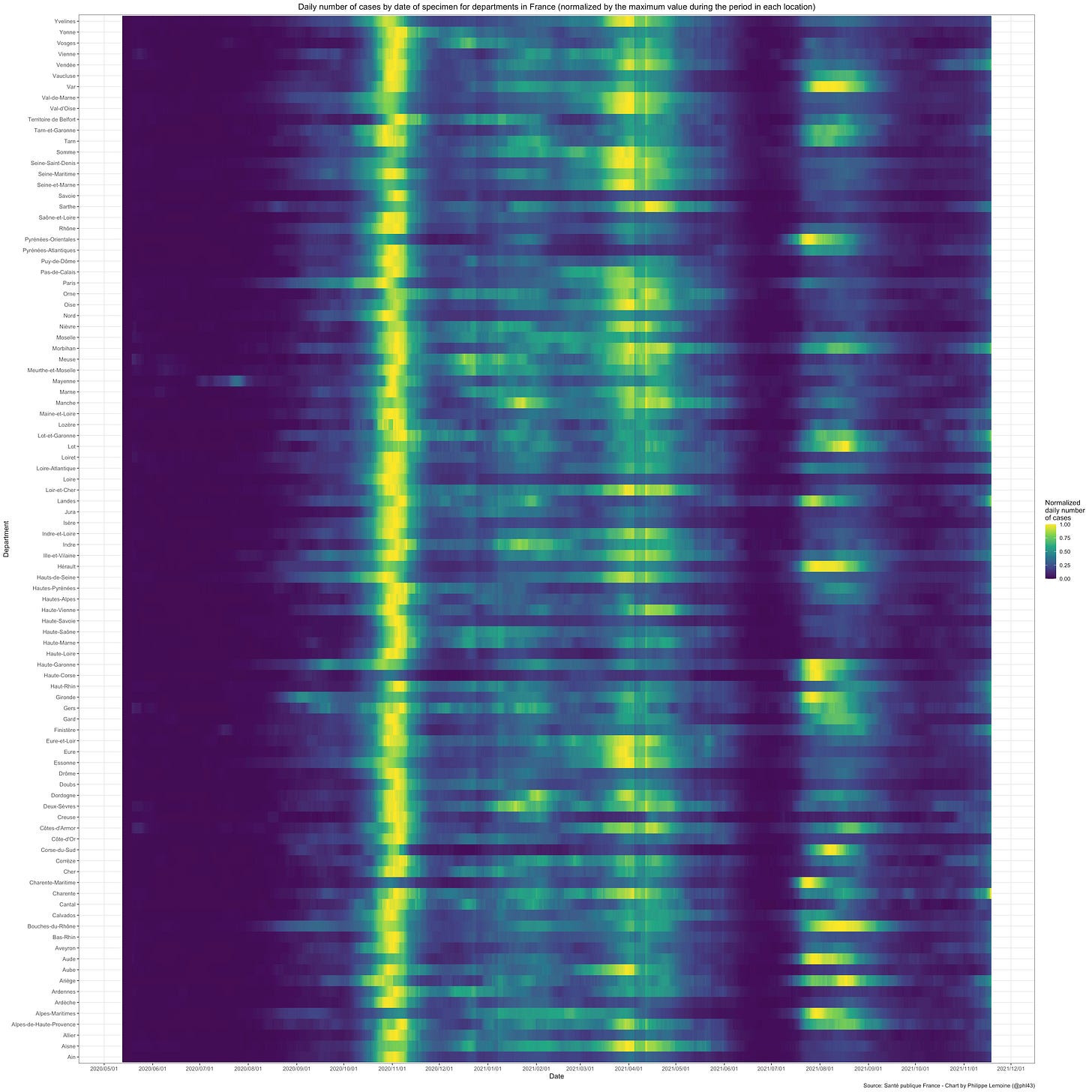
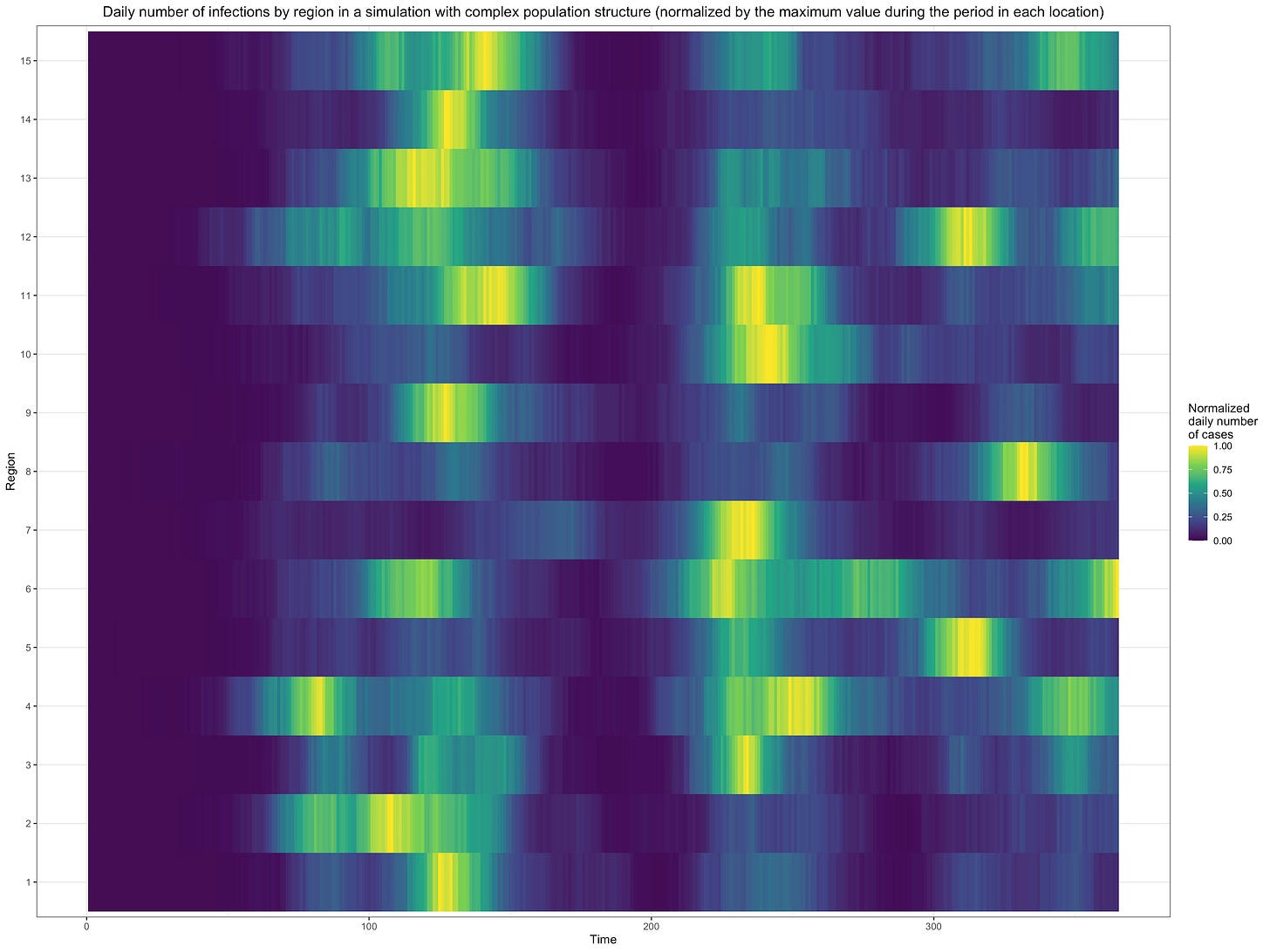
Moreover, the hypothesis that populations are structured in the sort of way assumed by the model is hardly obvious and, until we have evidence bearing directly on that, it will remain a conjecture. Unfortunately, we may never have evidence bearing directly on that, because it’s doubtful that we’ll ever have the kind of data we’d need to construct a graph that summarizes the pattern of interactions between individuals that can result in transmission.²⁹ One reason to be skeptical of this hypothesis is that, in most countries, waves of infections have been synchronized to a significant extent across regions. For instance, here is a figure that shows the daily number of infections over time in each French department relative to the maximum incidence reached in that department over the whole period, which starts after the first wave and runs until now:

As you can see, waves of infections tend to be synchronized across departments, but the extent to which this is true varies a lot depending on the wave. Thus, incidence peaked around the same time in almost every department during the second wave (at the beginning of November of last year), but there was less synchronicity during the third wave (which peaked between the end of March and April of this year) and even less during the fourth wave (which peaked in August of this year). The dataset doesn’t cover the first wave, but judging from the data on deaths, the amount of synchronicity it exhibited must have been somewhere between the third and fourth wave. I used French data to illustrate this point, but data from other countries show something very similar.

Now, for the kind of population structure I have suggested to explain this synchronicity, it has to be the case that subpopulations inside each subnetwork are distributed across several regions, because otherwise incidence would peak at very different times in different regions and waves would not be correlated across regions as much as they are. In other words, the population in each region must be distributed into different subnetworks that cut across regional boundaries, which many people will no doubt find implausible. For instance, what this means is that the population is structured in such a way that it’s sometimes easier for the virus to spread from a part of the network consisting of people who live in Paris to another part of the network consisting of people who live in Bordeaux than for it to spread from the former to another part of the network consisting of people who also live in Paris, even though Bordeaux and Paris are several hundreds of kilometers apart. Now, to be clear, I do not deny that intuitively this seems implausible. In fact, when I first considered the possibility that population structure might explain the cyclical dynamic of the epidemic about a year ago, I rejected it precisely for that kind of reasons, but I changed my mind since then for several reasons. First, while this objection has intuitive force, I don’t think we have any reason to trust our intuition on this issue. Indeed, each one of us is only familiar with a minuscule part of the network since we only know what kind of interactions we have with a handful of people and at best what kind of interactions some of them have with even fewer people, but in order to know whether the population has that kind of structure we’d have to be able to know the whole network, so I don’t see why anyone should trust their intuition on this question. In the absence of data bearing directly on that issue, the only thing we can go off is explanatory power, but I don’t know any other theory that can explain more parsimoniously why the effective reproduction number sometimes undergoes large fluctuations in the absence of behavioral changes.

Moreover, as I already noted, I am not claiming that population structure is the only factor explaining the dynamic of the epidemic. In particular, I don’t question that people’s behavior also matters a lot, so it’s not as if population structure had to explain everything on its own.³⁰ I would expect population structure to matter relatively less for waves that are more synchronized across regions and relatively more for waves that are less synchronized across regions. Simulations show that, even if you assume that the subpopulations in each subnetwork are to a large extent concentrated in just one region, it’s easy to obtain the amount of synchronicity we observe in real data except for the most highly synchronized waves. For instance, here is a graph that shows what happens when I randomly distribute the subpopulations in the network used for the simulation I presented above into 15 regions, randomly assigning a region to each subnetwork and assuming that each subpopulation in that subnetwork has a probability of 2/3 to be in that region while the rest of the probability is distributed uniformly across the other regions:

As you can see, even when I assume that subnetworks are heavily concentrated in one region, we can still end up with something that looks a lot like the synchronicity we find in real data. Thus, I don’t think the objection based on how synchronized waves in real data are is very powerful, at least as long as we don’t claim that population structure is the only factor driving the dynamic of the epidemic.

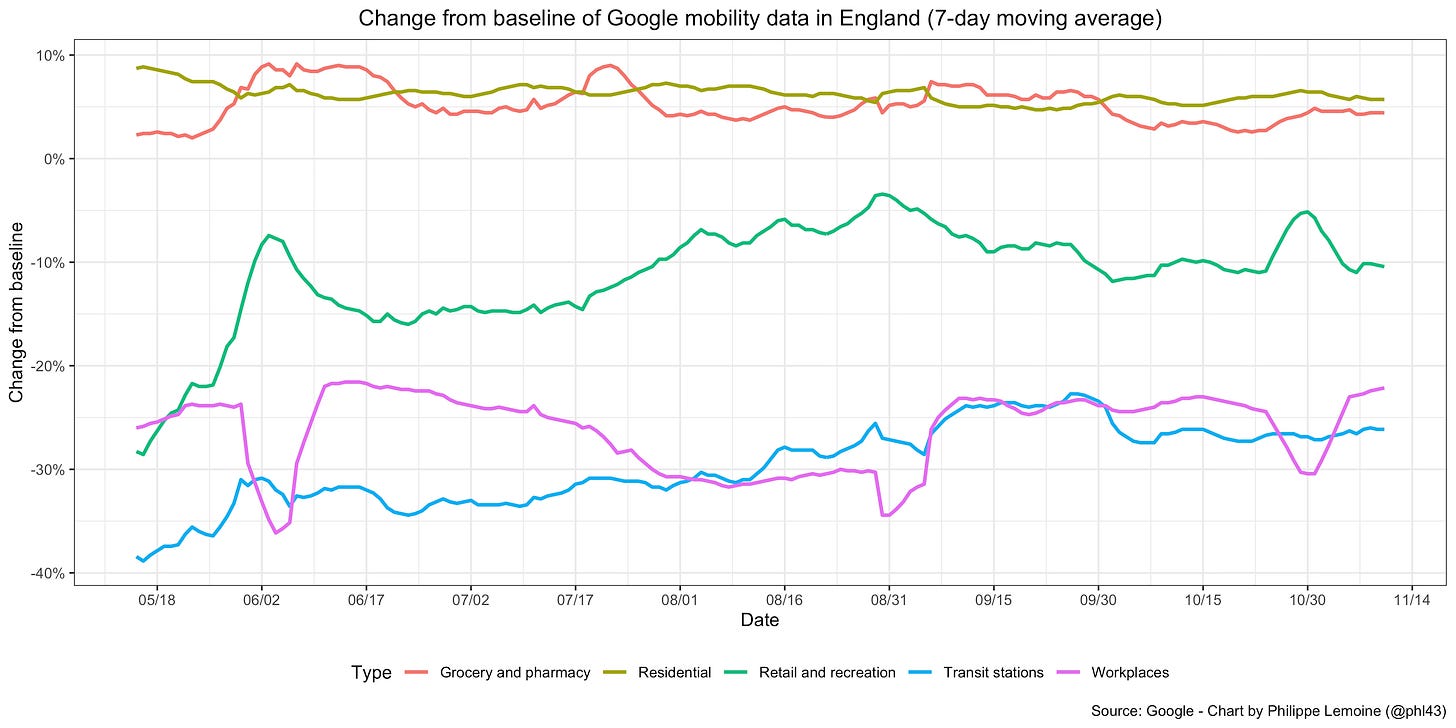
Again, ultimately the hypothesis that population structure has been a significant factor driving the dynamic of the epidemic will remain conjectural until we get data that bear directly on it, which may never happen. In any case, as long as we don’t have such data, we have to consider how much explanatory power each alternative theory has. Now, not only can this theory explain the fact that the effective reproduction number often undergoes large fluctuations despite the apparent lack of behavioral changes better than standard epidemiological models, but this isn’t the only phenomenon it could help to explain. For instance, most people have been surprised that, even after the vast majority of their population has been vaccinated, many countries still experienced large outbreaks. The most striking example, though hardly the only one, is the large wave that started in England this summer and is still ongoing:

The prevalence of people with antibodies against SARS-CoV-2 in England at the end of June was estimated at 91.9% among people 16 and over. If we assume that 25% of people under 16 in England had been infected by that point and that everyone who tests positive for antibodies is immune, this implies a prevalence of immunity of approximately 79% in the population as a whole, which is well above the herd immunity threshold predicted by standard epidemiological models unless we assume a very high basic reproduction number.³¹ For instance, in the SIR model, the virus would need to have a basic reproduction number of more than 5 for a country where 79% of the population is immune. If you complexify the model a little by taking into account different age groups, but still assume that people in the same age group mix homogeneously, the basic reproduction number you have to assume is even higher.

It’s true that the Delta variant that was associated with the latest wave in England is widely believed to be more than twice as transmissible as the original strain, which probably implies a basic reproduction number greater than 6 in England, but as I argued at length elsewhere, Delta’s transmissibility advantage is probably vastly overestimated. Moreover, even if I’m wrong about that, the basic reproduction number in the sense that is relevant for this discussion is not a fixed quantity but depends on people’s behavior. Now, as you can see on this chart, mobility data show clearly that even now people in England still have not returned to their pre-pandemic behavior:

Thus, even if Delta were really twice as transmissible as the original strain, this presumably would translate into a basic reproduction number much smaller than estimates obtained by multiplying the basic reproduction number at the beginning of the pandemic by 2.³² For instance, if we assumed that Delta would have a basic reproduction number of 6 under the conditions that prevailed in England before the pandemic, the fact that people still haven’t returned to their pre-pandemic behavior would only need to reduce it by less than 15% for England to be above the herd immunity threshold this summer, which is hardly inconceivable.³³ Of course, if I’m right that Delta’s transmissibility advantage has been significantly overestimated, it’s even harder to make sense of what happened in England within the traditional modeling framework.

Now, my argument so far has implicitly relied on the assumption that people who have recovered or have been vaccinated can’t be infected again, but the protection conferred by immunity, whether naturally acquired or induced by vaccination, is not perfect and it seems to wane over time, so this is not true. Standard epidemiological models can be modified to relax this assumption and, if you assume that vaccine efficacy wanes quickly enough, it’s possible to explain English data without assuming an implausibly high basic reproduction number. However, while I do not doubt that more transmissible variants and waning are part of the story here, I still think that, unless you model complex population structure, you have to make rather implausible assumptions to make sense of large outbreaks in places where the rate of people who have antibodies against SARS-CoV-2 is very high. Again, the point is not that models that make the homogeneous mixing assumption or something close to it can’t explain the data, which is trivially false because as I have already noted standard epidemiological models are remarkably flexible and it’s always possible to make them fit the data. The problem is that, in order to do so, you often have to make assumptions that are implausible. In the case of the assumptions you have to make to explain why places where the prevalence of immunity was very high nevertheless experienced large outbreaks, I don’t think it’s as clear-cut as when you have to assume massive behavioral changes even though mobility data don’t show any, but I still think that you have to make dubious assumptions. On the other hand, if the population has the kind of structure I have assumed in my simulations, then it’s not surprising that places where the prevalence of immunity is much higher than the herd immunity threshold predicted by standard epidemiological models can nevertheless experience large outbreaks, because that’s exactly what is going to happen if part of the networks that had been spared so far are seeded. To be clear, I do not doubt that more transmissible variants and waning are part of the story, I just think that population structure could be another part of it. In fact, just as the effect of behavioral changes on transmission can be mediated in part by the effect it has on the topology of the network on which the virus is spreading, the emergence of more transmissible variants and the waning of immunity can affect transmission not just directly but also through the effect they have on that topology.

Another phenomenon that is even harder to explain within the standard modeling framework, which I already discussed at length before, is the way in which Delta and before that Alpha replaced previously established lineages in most countries. The standard view is that both of them had a very large transmissibility advantage over previously established strains of the virus. In other words, other things being equal, people infected by Alpha cause more secondary infections than people infected by previously established variants and people infected by Delta cause more secondary infections than people infected by Alpha and the other variants that coexisted with it. The estimates of this transmissibility advantage vary wildly for both Alpha and Delta, but the estimate of 50% seems to have stuck in both cases for no particularly good reason that I can see, which is why people often say that Delta is more than twice as transmissible as the original strain of the virus. The problem with that standard view is that it can’t explain why both Alpha’s and Delta’s transmission advantages relative to previously established strains have been fluctuating wildly over time and space. For instance, here is a chart that shows Delta’s transmission advantage over previously established variants across French departments earlier this year, plotted against the prevalence of that lineage in each department during each period:

As you can see, not only is there a clear downward trend as the lineage becomes more prevalent, but at any point in time the estimates of Delta’s transmission advantage vary wildly across departments.

As I also noted at the time, the same thing happened before with Alpha, not just in France but also in the UK. In fact, if we look at Alpha’s and Delta’s transmission advantages in the UK, we also see them undergo wild fluctuations over both time and space:

On the standard view, it’s hard to see how this extreme variability of Alpha’s and Delta’s transmission advantages could be explained in a model that assumes the population is mixing homogeneously.³⁴ You would have to assume that mysterious factors present in some places but not in others or during some periods but not others had a massive effect — much larger than Delta’s alleged transmissibility advantage or even than the ridiculously large effect that some studies ascribe to non-pharmaceutical interventions — on Delta’s transmission but not on the transmission of the other variants or the other way around.

On the other hand, as I explained in my post about Delta’s transmissibility advantage, there is nothing particularly surprising about this variability if the population is structured in networks that are internally well-connected but loosely connected to each other. The idea is that, if different variants don’t spread in the same networks and some of them spread in networks where the prevalence of immunity is low because they had been relatively spared so far, a variant’s transmission advantage over the other strains of the virus can significantly overestimate its transmissibility advantage. Indeed, in that case, it will spread much faster relative to other variants than it would have other things being equal, because it’s spreading in networks where the prevalence of immunity is lower than in the networks where other variants are spreading and things are therefore not equal. Thus, it’s crucial to distinguish a variant’s transmission advantage over another (i. e. how fast it’s actually spreading relative to it) from a variant’s transmissibility advantage over another (i. e. how fast it would spread relative to it other things being equal), because they can diverge radically in the presence of complex population structure. This could also explain why, in France, both Alpha’s and Delta’s transmission advantage collapsed after the initial phase of expansion. This is what you would expect if a new variant initially expanded in networks where the prevalence of immunity was relatively low, while the previously established variants had nearly exhausted the pool of susceptibles in the networks where they are spreading, because they have been circulating for longer. Moreover, because there is no reason to expect that subpopulations in each network are distributed uniformly across regions and, on the contrary, every reason to expect them to be heavily concentrated in one region, it’s also entirely unsurprising if the population is structured in that way that a variant’s transmission advantage varies wildly across regions.

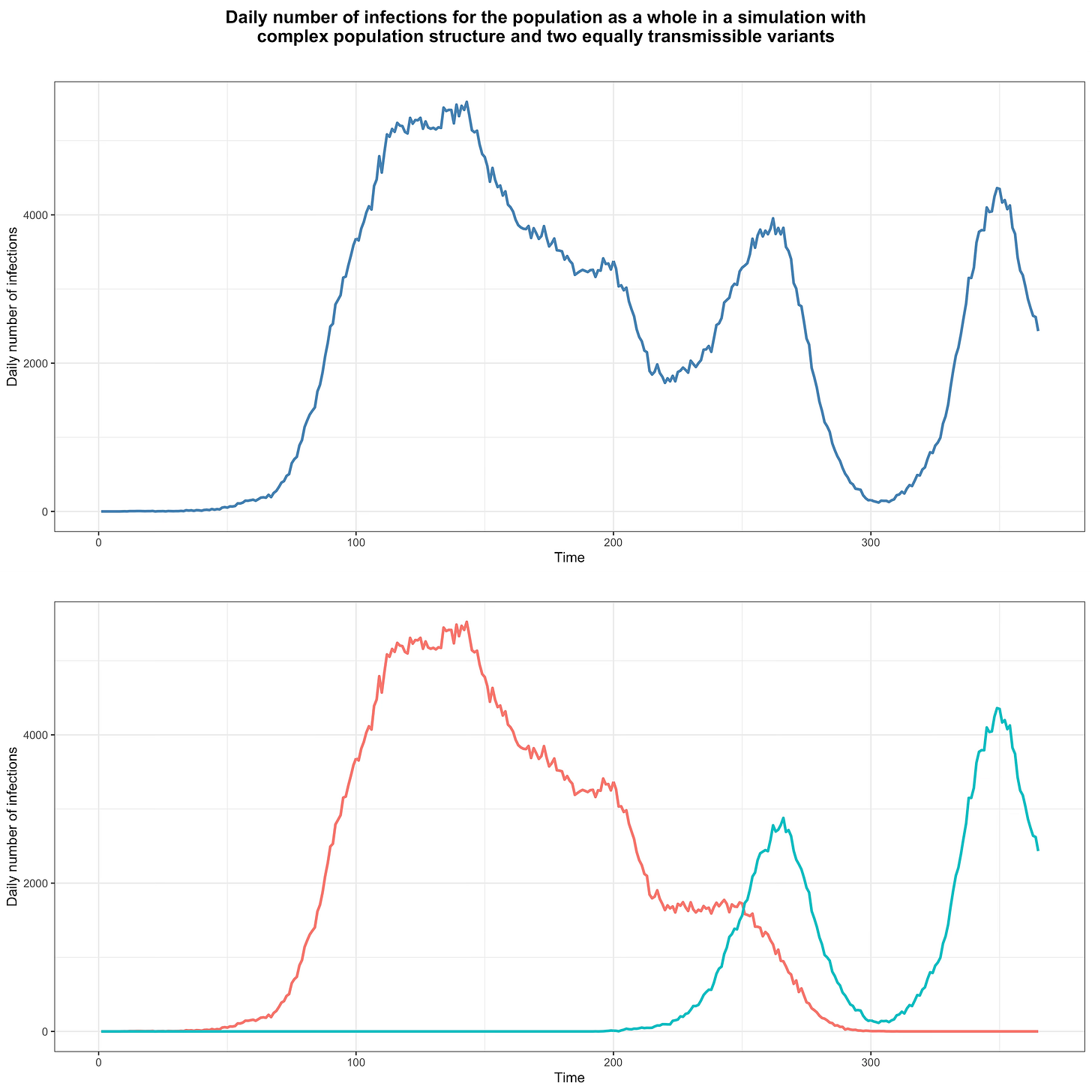
At the time, I laid out the argument in purely intuitive terms, but now I can back it up with simulations. In order to show that one variant could easily have a very large transmission advantage over another without being intrinsically more transmissible, I used the same model as above, randomly generating a network of subpopulations in the same way. However, instead of seeding the network with the same variant for the whole duration of the simulation, I seeded it with one variant during the first 150 days and, starting on the 180th day, with another for the rest of the simulation. Crucially, I have assumed that both variants have exactly the same basic reproduction number in each subpopulation, so by assumption neither has any transmissibility advantage over the other. This figure shows the daily number of infections in that simulation, with infections for both variants summed in the upper panel and disaggregated in the lower panel:

As you can see, after the population is no longer seeded with the first variant, it continues to circulate for a while but after about 150 days it can’t find anyone susceptible in the networks where it was spreading anymore and dies out. Meanwhile, after the second is introduced into the population, it eventually reaches a network where the prevalence of immunity is low and starts new waves of infections.

If we compute the transmission advantage of the second variant over time, keeping only observations with at least 100 infections for each variant (in order to eliminate any large fluctuations that might occur at low incidence due to the stochastic nature of the transmission process), here is what it looks like:

As you can see, although by assumption both variants are equally transmissible, the second variant nevertheless has a very large transmission advantage that undergoes large fluctuations over time but trends downward.³⁵ This demonstrates that, even if a variant has no transmissibility advantage whatsoever over another, it can still have a large transmission advantage over it because it’s spreading in networks where the prevalence of immunity is lower. Of course, as I explained in my post on Delta’s transmissibility advantage, I don’t claim that Alpha and Delta have no transmissibility advantage, but that it has been largely overestimated because people have been careless in inferring a transmissibility advantage from the observed transmission advantage, which as this simulation shows can easily diverge radically from the transmissibility advantage because populations don’t actually mix homogeneously.

I also computed the second variant’s transmission advantage separately in each region, after randomly assigning regions to subpopulations in the same way as before. In order to do that, I only kept observations with at least 25 infections for each variant and excluded regions in which that left less than 20 observations (this removed 3 regions out of 15), to avoid the extreme variability that can be caused by the stochastic process of transmission at very low incidence.³⁶ As you can see, as in real data, we find even more variability than at the aggregate level:

Thus, not only can population structure explain why the effective reproduction number can undergo large fluctuations even in the absence of significant behavioral changes, but it can also make sense of the wild variability of Alpha’s and Delta’s transmission advantages, which standard epidemiological models that make the homogeneous mixing assumption can’t. The fact that epidemiologists have largely ignored this variability doesn’t negate this advantage of my theory, because they shouldn’t have ignored it and, if they have, it’s probably in large part precisely because it’s impossible to make sense of it within the traditional modeling framework. Again, this doesn’t prove that my theory is correct, but I think it’s enough to seriously consider the possibility that complex population structure of the sort I assume in my simulations plays a significant role in the real world and to ponder what implications it would have if that were true, which is what I turn to in the next section.

Have we been thinking about the dynamic of the pandemic in the wrong way all this time?

If real populations have the kind of structure my theory posits, then a lot of what people who study the pandemic have been doing is completely wrong. Thus, if I’m right that we should take that hypothesis seriously, it should at least make everyone nervous. First, since the beginning of the pandemic, we have been obsessed by quantities — the effective reproduction number and the herd immunity threshold — that are essentially meaningless at the aggregate level in a model with complex population structure. In the modeling framework I have used above, they make sense at the level of subpopulations, but at the aggregate level they are uninterpretable or misleading if we interpret them as if the virus were spreading in a homogeneous mixing population. As we have seen, not only can incidence fall even in the absence of behavioral changes when the prevalence of immunity is much lower than the herd immunity threshold predicted by a model with homogeneous mixing or something close enough (because the virus has exhausted the pool of susceptibles in one part of the network and wasn’t able to reach another part from there before this happened), but it can also rise when the prevalence of immunity is significantly above that threshold (because there are still parts of the network where most people do not have immunity). Similarly, while the effective reproduction number may be meaningful for parts of the network that can be idealized as homogeneous mixing populations (as I have done for my simulations), at the level of the population as a whole it just aggregates the dynamics of the epidemic in different parts of the network and doesn’t have the meaning that has been ascribed to it by everyone since the beginning of the pandemic. In particular, changes in the effective reproduction number at the aggregate level cannot be interpreted as a sign that people change their behavior in a way that affects transmission, that non-pharmaceutical interventions work or don’t work, etc. Yet this is what everyone has been doing for more than a year and a half and it’s what everyone is going to keep doing this winter.

The problem is not limited to journalists and public officials, who have spent the entire pandemic trying to read some kind of causal story into changes of the effective reproduction number, it also affects the scientific literature on the pandemic, which has been used to guide policy. Indeed, if the population has the kind of structure I have proposed, then not only are the methods used to estimate the impact of non-pharmaceutical interventions, behavior and even vaccination on transmission completely unreliable, but so are the projections based on the estimates that were obtained with those methods. As I have explained before, studies on the impact of non-pharmaceutical interventions can roughly be classified into 2 groups, depending on whether they assume a particular epidemiological model or use seemingly more agnostic econometric methods to estimate the effects of non-pharmaceutical interventions. The first type of study basically asks what effect non-pharmaceutical interventions must have had on transmission to explain the data if we assume they were generated by a standard epidemiological model. Thus, if the daily number of infections went down before the herd immunity threshold implied by the model was reached, this method will ascribe a large effect to whatever non-pharmaceutical interventions started around that time, because that’s the only way it can fit the data. But what if the data were not generated by a standard epidemiological model, with a homogeneous or quasi-homogeneous mixing population? In that case, this method may also find that non-pharmaceutical interventions had a very large effect, even if they only had a small effect or no effect whatsoever! In particular, if the population has the kind of structure I have assumed for my simulations, this method may conclude that non-pharmaceutical interventions have a very large effect even if they didn’t have any or only a small one. The most famous example of this type of study, which may also be the most cited paper during the pandemic (it has already been cited 1,662 times as I write this), is Flaxman et al. (2020), which I have already criticized in detail elsewhere. However, it’s hardly the only example, there are dozens and probably hundreds of others that use the same method.

In order to illustrate the problem with this method, I fitted a standard epidemiological model with homogeneous population mixing to the first 200 days of data (corresponding to the first wave) from the simulation with complex population structure and a single variant I presented above, but I told the model that a lockdown was in effect from the 105th day and that it wasn’t lifted until 2 months and a half later:

Of course, no lockdown whatsoever played any role in the data generating process, but the model doesn’t know that, so it tries to figure out what effect this non-existent lockdown must have had on transmission to fit the data as best it can on the assumption that the virus was spreading in a homogeneous mixing population.³⁷ What it concludes is that the lockdown reduced transmission by more than 40%. Thus, although there was no lockdown and therefore its real effect was zero, using the same method that epidemiologists have used in countless studies since the beginning of the pandemic, I find that it had a very large effect. This is because the model wrongly assumes a homogeneous mixing population, so it assumes that herd immunity hasn’t been reached yet, but in fact it has been reached in the part of the network where the virus was spreading during the first wave. As a result, it ascribes this reduction of transmission to the lockdown (which didn’t even happen and therefore had no effect whatsoever), even though it was the effect of population structure. Thus, if the population has the kind of structure my theory posits, this method will be completely unreliable, yet dozens of studies have used it to estimate the impact of non-pharmaceutical interventions since the beginning of the pandemic.

The other type of studies that estimate the effects of non-pharmaceutical interventions use a more traditional econometric approach. Roughly, instead of assuming a particular epidemiological model that includes parameters for the effect of non-pharmaceutical interventions and fitting epidemic data to that model, they look for correlations between non-pharmaceutical interventions and the growth of the epidemic. On the surface, this approach seems more agnostic than the previous one, but this is largely an illusion. While this method doesn’t require that one explicitly make strong mechanistic assumptions about the data generating process, if the effects are to be interpreted causally, one still has to make strong assumptions about that process. While many papers using that approach keep those assumptions implicit, a paper by Chernozhukov et al. I criticized a few months ago actually spelled them out explicitly by using the SIR model to motivate their econometric model, which makes clear that it rests on the homogeneous mixing assumption.³⁸ It’s actually not hard to understand intuitively why, if this assumption doesn’t hold, their model and similar econometric approaches will not be able to recover the causal effects of non-pharmaceutical interventions. As we have seen, in the presence of complex population structure, the effective reproduction number can undergo large fluctuations even without any behavioral changes. For instance, it can suddenly fall because the virus has exhausted most susceptibles in a part of the network, but failed to reach another part of the network with more susceptibles from there. Therefore, if a non-pharmaceutical intervention happened to be in place around the time this happened, there will be a correlation between that non-pharmaceutical intervention and the growth of the epidemic. This correlation will be interpreted as the causal effect of the non-pharmaceutical intervention, even if it didn’t have any causal effect on transmission. In theory, this could also bias the estimate of the effect of non-pharmaceutical interventions in the other direction and make one conclude that non-pharmaceutical interventions increase transmission, but in practice I think it’s unlikely since decision-makers typically order non-pharmaceutical interventions when incidence has reached a high enough level and tend to keep them in place for a relatively long time after it has started to go down.

We can also illustrate this point by fitting a simple version of the model used in Chernozhukov et al. (2021) to the same data I used above to show that the method used in Flaxman et al. (2020) was not reliable when the homogeneous mixing assumption doesn’t hold and the virus is spreading in a population that has strong community structure.³⁹ This model leverages the variation of non-pharmaceutical interventions across time and regions to estimate the effect they have on the daily growth rate of infections by looking at how the presence or absence of non-pharmaceutical interventions is related to that variation.⁴⁰ I randomly drew a date between the 100th and 140th day of the simulation in each region, told the model that a lockdown was in effect in that region for 60 days starting from that date and the model used that information plus the data on infections to estimate the effect of this non-existent lockdown. I repeated this procedure 1,000 times and here is the distribution of the estimates it found:

As you can see, according to the model and depending on when the lockdown was supposed to be in effect in each region, a lockdown that never took place and therefore had no effect whatsoever reduced the daily growth of infection by 7% to 10%. Not only is this a very large effect, but it was statistically significant at the conventional 0.05 level in every single case, which shows that the kind of model used in Chernozhukov et al. (2021) is completely unreliable in the presence of complex population structure of the sort that is assumed by the model used to generate the data.

This discussion illustrates a deep point, which most scientists understand but the public does not, namely that statistics can only help you to answer questions about the world by making assumptions about the world. If those assumptions are false, the answers it gives you cannot be trusted. For instance, in the case of the methods used above to estimate the effect of a lockdown, the model assumes that the virus spreads in a homogeneous mixing population. If that assumption is true or close enough to the truth, it may allow you to estimate the effect of a non-pharmaceutical intervention pretty accurately, but if that assumption is completely false, as is the case in the data I generated with a model that assumes the virus is spreading in a network of homogeneous mixing subpopulations that can be divided into subnetworks that are internally well-connected but only loosely connected to each other, then it will produce completely unreliable estimates, as we have just seen. Indeed, while it’s true that the effect of the lockdown is estimated from the data, it’s not estimated just from the data, because the estimation also relies on the assumptions that are made about the data generating process. This is always the case, because you can never estimate a causal effect just from the data and you always need to make assumptions about the world. Unfortunately, most people don’t realize that, so they think that the results of empirical studies can be taken at face value because the effects of such-and-such intervention was estimated “from the data”.

In the case of studies that estimated the effect of non-pharmaceutical interventions on transmission, homogeneous population mixing was usually assumed (regardless of whether the authors realized it and whether they realized that it was not a trivial assumption), so if I’m right that we have good reasons to think that real populations depart significantly from that assumption, we cannot trust their conclusions. Note that I’m not even saying their conclusions are false, although I think they are (as I have explained at length before there are other reasons to think so beside the fact that real populations are not mixing homogeneously), I’m just saying that we have no reason to be confident they are true because we have no reason to think the homogeneous mixing assumption on which they rest is close enough to the truth for the methods they use to be reliable, which is a much weaker claim. Even if that assumption is close enough to the truth, the fact that we don’t know that and that we even have good reasons to doubt it should result in a healthy dose of skepticism toward studies that implicitly rely on it, but unfortunately neither experts nor public officials have demonstrated much skepticism about their conclusions. In fact, they have used the results of those studies — which are sometimes comically bad even if you set aside the issue of the homogeneous mixing assumption — to make projections that were used to guide policy, which may be part of why those projections have systematically and massively failed since the beginning of the pandemic. If the population has the kind of structure posited by the theory I explored above, then it’s not surprising that projections were so unreliable. Indeed, if the virus spreads on a network that has that kind of community structure, then at best aggregate-level statistics can be used to forecast the short-run evolution of the epidemics (as some machine-learning techniques have been able to do with a measure of success), but any attempt to forecast the epidemic beyond that is pointless because there is no way to predict if or when the virus will reach another part of the network where it will find enough susceptibles to expand again.

Conclusion

I have argued that, while there are solid theoretical reasons to think that ultimately the dynamic of the epidemic depended on people’s behavior, there is also strong evidence that the effective reproduction number sometimes underwent large fluctuations that could not be explained by changes in people’s behavior. The cyclical nature of the epidemic has often been noted, but except for the vague claim that respiratory infections are “seasonal” (which is true but doesn’t actually explain much), nobody has really tried to explain it. In this post, I have proposed that population structure could be part of the explanation, because real populations are not homogeneous mixing. This theory can explain why, although ultimately transmission depends on people’s behavior, the effective reproduction number can undergo large fluctuations even in the absence of behavioral changes. While there is no evidence bearing directly on this hypothesis one way or the other, it can explain many phenomena that are difficult to explain with standard epidemiological models, which assume homogeneous mixing or something close to it. Of course, this doesn’t mean that other factors, such as behavioral changes but also more transmissible variants, vaccination and meteorological variables, don’t also play a role, which I’m sure they do, but I think that we should at least take the possibility that population structure plays a large role seriously. Indeed, even if this possibility turned out to be false, the fact that we have good reasons to believe it’s true should lead us to question how we have been thinking about the pandemic so far. If real populations are structured in the way my theory posits, not only are several quantities, such as the effective reproduction number, we have been obsessing over largely meaningless at the aggregate level, but the methods used in the literature to estimate the effect of non-pharmaceutical interventions, vaccinations, etc. could be totally unreliable. This suggests that we should build the capacity to collect data about the characteristics of the network on which infectious diseases spread, so that when the next pandemic hits, modeling can take into account population structure and therefore produce better projections and more reliable estimates of the impact of interventions.

Addendum on the relationship between the hypothesis discussed in this post and the earlier debate about the effect of heterogeneity in social activity

Based on the response to this post, many people seem to think what I’m saying is the same thing as what people who argued back in 2020 that heterogeneity in social activity might lower the herd immunity threshold, but while this is related to what I’m talking about here it’s actually different so I thought it might be useful to briefly explain why. I’m actually familiar with the debate that took place about that last year, since I even wrote a post about it at the time. In both cases, the point is that heterogeneity affects the dynamic of the epidemic, but it’s not the same kind of heterogeneity. What people were arguing last year is that, if people’s level of social activity varies a lot, herd immunity will be reached sooner because the people who spread the virus the most are also the most likely to be infected early in the pandemic.⁴¹ This intuitive argument is supported by models showing that, when you introduce that kind of heterogeneity, herd immunity does in fact occur sooner. If we model the spread of the virus on a network, this debate was mostly about the degree distribution, i. e. the distribution of the number of edges connected to each individual in the network. The point was that, when this distribution is more dispersed than standard epidemiological models implicitly assume, the herd immunity threshold will be lower than predicted by those models.

However, the kind of epidemic behavior I discuss in this post only arises when the network has community structure, which is about a lot more than the variance of the degree distribution.⁴² In particular, the network must exhibit a specific kind of clustering, but this doesn’t just depend on its degree distribution. In fact, it’s conceivable that at the level of the parts of the network that I idealized as homogeneous mixing population in my simulations, the herd immunity threshold is lower than predicted by standard epidemiological model due to heterogeneity in social activity, even though at the aggregate level it’s higher due to community structure, as I explained above. So while most people have interpreted the fact that many places with a high prevalence of immunity have recently experienced large outbreaks as proof that people who argued that heterogeneity in social activity could lower the herd immunity threshold were wrong, this is not actually the case if the network on which the virus is spreading has the kind of structure assumed in this post. Of course, like the rest of this post, this is very speculative, but it goes to show that the spread of infectious diseases is a lot more complicated than people generally assume.

Addendum on what I expect the import of population structure to be going forward

As I have explained before, the pandemic is on its way out and the virus is going to become endemic, though not every place is at the same stage of that transition. If I’m right that population structure has played a key role in the dynamic of the pandemic so far, what role should we expect it to play as the virus becomes endemic? I haven’t tried to model this, but it’s an interesting question, so I figured that it would be useful to add a few words about this. Basically, while I expect that population structure will continue to be relevant even after the virus has become endemic (because the population still won’t be homogeneous mixing), I also expect that it will become less relevant as we get closer to the endemic equilibrium and that seasonal effects due to meteorological variables will progressively become dominant. This is what I expect mainly for 2 reasons. First, as more and more people have been infected or vaccinated, the different parts of the network will become more homogeneous in terms of susceptibility to infection. Second, although the population will not magically become homogeneous mixing as the virus becomes endemic, I nevertheless expect that it will get closer to this idealization because once people go back to their regular behavior it will presumably increase connectivity between different parts of the graph. So eventually I think it will leave other factors, mainly seasonal effects due to the direct and indirect effects of meteorological variables but also the occasional emergence of new variants that are more transmissible or better able to evade prior immunity, will dominate the effect of population structure and the occurrence of waves will become more reliably predictable.

1. This value of the dispersion parameter was taken from Endo et al. (2020) and implies that about 10% of infected people are responsible for 80% of secondary infections. See Lloyd-Smith et al. (2005) for the logic behind modeling secondary transmission with a negative binomial distribution.

2. I used the meta-analytic estimate of the generation time in Challen et al. (2020) for this distribution.

3. In theory, non-pharmaceutical interventions and voluntary behavioral changes can reduce transmission not only by reducing the rate at which infectious people interact with other people, but also by modifying the nature of the interactions people have in a way that reduces the probability of infection per contact. For example, people may decide to meet outdoors more often because they know that it’s easier to get infected indoors, yet still meet as often as before.

4. To be clear, as I argued before, I don’t believe that lockdowns are nearly as effective as that. I just assume the lockdown has a very large effect to illustrate what happens in a model of this sort if the basic reproduction number suddenly falls.

5. It takes a few days in the simulation because, as we have seen above when I described the model, for each person infected at time T, the model computes at time T how many people he will infect and when they will be infected based on the basic reproduction number at time T. Therefore, by the time the lockdown comes into effect, the number and timing of infections caused by people infected before that have already been decided using the basic reproduction number prior to the lockdown. I won’t go into the details here, but this shortcut allows me to model secondary infections and superspreading in a computationally efficient way, at the cost of creating this kind of lag when the basic reproduction number changes over time.

6. However, as long as the herd immunity threshold has not been reached, even if the epidemic has been extinguished during the period when the effective reproduction number was temporarily pushed below 1, incidence will start growing again as soon as the virus is reintroduced. Things are a bit different in a stochastic model, because in such a model infectious people may not infect anyone due to chance so a non-zero number of people in the infectious compartment doesn’t ensure that a large epidemic will occur even if the basic reproduction number is greater than 1, but it doesn’t matter here.

7. I’m using data on ICU admissions rather than cases because Sweden was testing very little during the first wave and, as a result, the data on cases reflect more changes in testing than changes in incidence during that period.

8. However, it means that studies that attempt to estimate how many lives non-pharmaceutical interventions had saved by assuming that, in the absence of non-pharmaceutical interventions, people’s behavior would not have changed wildly overestimate the impact of non-pharmaceutical interventions. This point is so obvious that you would think it’s unnecessary to make it, but you would be wrong, since many studies on the impact of non-pharmaceutical interventions make precisely this mistake, including what is probably the most cited study on that question.

9. For instance, see this timeline of emergency orders in Miami-Dade County, the county with the largest population in Florida. For statewide restrictions during this period, see this Wikipedia page, which also has some information on some local measures.

10. On the other hand, the fall of the effective reproduction number that started at the end of October closely follows a drop in mobility, so behavioral changes could explain why the second wave started to recede when it did.

11. See Gatalo et al. (2021) and Badr and Gardner (2020) on how the relationship between mobility and epidemic growth changed over time in the US and Nouvellet et al. (2021) for a similar finding in a dataset of 52 countries around the world.

12. On the impact of meteorological variables on transmission, see Damette et al. (2021), Paraskevis et al. (2021) and Ma et al. (2021).

13. In the paper, they only analyzed data up to December and it’s not clear that it remains true after that, but this is hard to interpret because vaccination and the introduction of more transmissible variants could have affected the relationship between the contact index and the effective reproduction number.

14. I say that as someone who previously argued that voluntary behavioral changes were enough to explain why incidence started to fall long before the herd immunity threshold could plausibly be assumed to have been reached.

15. This point was made early by Noah Carl in a piece where he pointed out that incidence had declined in South Dakota despite very little behavioral change around the time when the effective reproduction number fell below 1.

16. Moreover, as I also noted above, at least part of the effect of meteorological variables is mediated by people’s behavior anyway.

17. In practice, most of the models that epidemiologists actually use to analyze real data or make projections relax that assumption somewhat by assuming that it only holds within age groups or that people differ in how much social activity they have (among other things), but this doesn’t affect the qualitative trajectory of the epidemic in a way that could explain the data, so I’m ignoring this fact in my presentation to keep things simple. In the framework I’m using below, this amounts to letting the virus spread on a very simple network with a handful of populations that are all connected to each other (although the edges have different weights), so there is no community structure and the peculiar epidemic behavior I discuss in this post cannot arise.

18. For a good, up to date and accessible review of the literature on epidemic processes in complex networks, I recommend that you read Pastor-Satorras et al. (2015), which I found very helpful.

19. The code for the simulations presented in this section, as well as for the figures shown elsewhere in this post, can be found in a GitHub repository.

20. If you want to learn more about random graphs, I recommend that you read Newman et al. (2001), which I found very useful.

21. Most real-world networks don’t have Poisson-distributed degrees, and the configuration model was developed precisely to allow for arbitrary degree distributions, but we have no idea what kind of degree distributions the sort of networks I consider here have, so to keep things simple I stuck with the simple case of Poisson-distributed degrees. However, since I used the configuration model to generate the subnetworks, it would be trivial to use another distribution.

22. The algorithm is actually written in such a way that, in theory, it could connect a node in one subnetwork to a node in another subnetwork, but in practice this is extremely unlikely.

23. Since the network is a graph of populations and not individuals, it would have made sense to generate a directed graph, but to keep things simple I only used undirected graphs.

24. The graph was generated with Yifan Hu’s algorithm in Gephi 0.9.2 using the algorithm’s default settings. The colors assigned to different subnetworks are not always easy to distinguish from each other because, with 100 subnetworks, it’s difficult to find enough colors that are visually distinct.

25. I’m using the word “travel” here, but keep in mind that, for reasons that will be explained below, both subpopulations and subnetworks may spatially overlap. Depending on what the graph of individuals that summarizes people’s patterns of interaction, which in the simulation is idealized as a network of homogeneous mixing populations, is like, people could be neighbors yet belong to different subpopulations or even different subnetworks.

26. Since each subnetwork is a random graph with a Poisson degree distribution of mean 5, about 99% of the subpopulations it contains are expected to be part of the giant component. In theory, even if a subpopulation is part of the giant component, it may never be reached by the virus since there is a non-zero probability that none of the people infected in one of the subpopulations to which it’s connected will travel to it and cause secondary infections if they do, but in practice the results of the simulation show that it almost never happens because the probability of travel within subnetworks is high enough. In each subnetwork, 5 subpopulations on average are connected to a subpopulation in another subnetwork and, because of what I just said, we may assume that all of them will be invaded by the virus in about 95% of the cases. As noted below, I assumed a basic reproduction number of 2.5 on average in each subpopulation, so the expected final attack rate in each subpopulation reached by the virus is about 89%. Since subpopulations have a size of about 520 on average, it follows that, for a subnetwork reached by the virus, we should expect approximately 2,500 people who belong to a subpopulation connected to a subpopulation in another subnetwork to be infected. Finally, since each of them has a probability of 1 in 10,000 of traveling along that edge, the probability that someone infected in one subnetwork will spend their infectious period in another subnetwork is about 25%. This is very much a back-of-the-envelope calculation, but it should be about right. However, keep in mind that most infected people never infect anyone, so the probability that someone infected in one subnetwork will travel to another subnetwork and will start a large outbreak over there is much less than 25%. In fact, since I use a negative binomial distribution with a dispersion factor of 0.1 to model secondary infections (which means that approximately 72% of people who are infected never infect anyone even if everyone in the population is susceptible), it will be about 7%.

27. However, they do not increase the size of those subpopulations, so effectively I’m assuming they just spend their infectious period over there before going back to where they came from. I made the same assumption for people traveling from one subpopulation to another within the network.

28. The simulation would be more computationally intensive, but it would not be very difficult to modify it to simulate several countries that, like subpopulations within a country, also form a network by seeding just one of them at the beginning of the simulation. In that case, instead of being exogenous, seeding from abroad at the level of each country would become endogenous to the model.

29. The closest thing I have seen are the cell phone GPS data used by the German study I already mentioned above, but it’s unclear whether even this kind of data will be sufficient. Nevertheless, the main author of that study told me that the network they had been able to construct based on those data clearly had community structure, but it’s difficult to interpret what this means and the authors are currently working on figuring that out.

30. In fact, as I noted above, taking into account population structure can help understand better how behavior affects transmission.

31. The Office for National Statistics estimated that, back in January (before anyone in that age group had been vaccinated except a handful of people with medical conditions that made them particularly vulnerable), 25.9% of people between 16 and 24 in England had antibodies against SARS-CoV-2. As in the rest of the world, younger people seem much more likely to have been infected in England, so the assumption that 25% of people under 16 had been infected by the end of June seems conservative.

32. In fact, it’s a conceptual error to talk about the basic reproduction number of a virus or a strain without specifying a population and a time, but it has become customary so I will avail myself to this linguistic sleight of hand with the understanding that the basic reproduction number is really a relational property between a virus, a population and a time.

33. You may be surprised that, after I argued that behavior couldn’t explain the fluctuations of the effective reproduction number, I’m saying that it could have a large effect on the basic reproduction number, but there is no inconsistency. There is absolutely no doubt that changes in behavior relative to the pre-pandemic period have a large effect on the basic reproduction number, but it’s still the case that behavior can only explain fluctuations of the effective reproduction number when it changes, and we have seen that it often doesn’t even as the effective reproduction number undergoes large fluctuations.

34. As I noted in my post on Delta’s transmissibility advantage, while some of this variability may be spurious and due to measurement error, measurement error can’t explain all or even most of it, so this is a real puzzle that needs to be explained and not merely a measurement artifact.

35. In order to minimize fluctuations due to chance, in addition to keeping only observations with at least 100 infections for each variant, I have also estimated the effective reproduction number for each variant over 7-day rolling windows.

36. Moreover, the effective reproduction number for each variant was again estimated over 7-day rolling windows, which has the effect of smoothing the transmission advantage curve.

37. The model was fitted by MCMC, which is short for “Markov chain Monte Carlo”. Roughly, it’s a statistical method that can be used to estimate the distribution of a model’s parameters, given the data and the assumptions you make about the distribution of the parameters before you have seen the data. Here the main parameter of interest is the effect of the fictional lockdown I told the model was in place for 75 days starting from the 105th day. The details of the model and the priors I used don’t really matter for the argument I’m making, so I skip them in my presentation, but you can check the code on GitHub if you’re curious.

38. Chernozhukov et al. recently published a response to my critique where they argue that it fails to undermine their conclusions. I don’t think their response shows that and will reply to it when I have time, but this post actually elaborate on a point I had only made in passing in my critique, because it shows that the assumptions on which their model relies are very uncertain and that if they don’t hold then we have no reason to trust their conclusions.

39. Even in a homogeneous mixing population, the model will deliver biased estimates if enough immunity has been accumulated in the population. Since with simulated data I can actually observe the number of infections, I could have controlled for that in the model, but I only used the first 200 days of data and just 12.3% of the population had been infected by that point so I didn’t even bother.

40. In their paper, Chernozhukov et al. use a variable that approximates the weekly growth rate of cases as the dependent variable of their regression, because data on cases are very noisy and looking at the weekly growth rate should remove some of that noise, especially that due to day-of-the-week effects on reporting. Since I’m using simulated data on infections without any noise, I don’t have this problem, so I’m using a dependent variable that approximates the daily growth of infections. I also included a region fixed effect in the model and clustered standard errors by region.

41. Actually, some people also talked about other kinds of heterogeneity, such as heterogeneity in susceptibility. If you are modeling the spread of a virus on a network, whose edges have a weight indicating the probability of transmission along that edge, this presumably depends on a combination of the degree distribution and the distribution of the weights. But this is also different from the kind of heterogeneity I’m discussing in this post.

42. In general, the topology of a network can’t be reduced to the properties of its degree distribution, because it depends on facts about how the network was generated that go beyond the degree distribution that was used.